Accuracy, precision, and recall

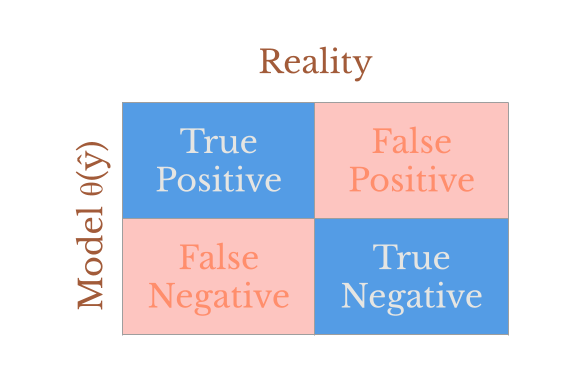
Accuracy

Formula

\[\dfrac{\text{True Positives} + \text{True Negatives}}{\text{Total number of samples}}\]

Interpretation

The proportion of correctly classified samples. It is an overall indicator of the model’s performance (irrespective of sample sizes and class/category (im)balance).

Caution

Accuracy ignores possible biases introduced by unbalanced sample sizes. I.e. it ignores the “two ways of being wrong” problem (see below).

Example

import numpy as np

N = 100
samples = np.array(["cat"] * 60 + ["dog"] * 40)
# Model always predicts cat
predictions = np.array(["cat"] * 85 + ["dog"] * 15)

print(f"Number of cats in sample: {np.sum(samples == 'cat')}")
print(f"Number of dogs in sample: {np.sum(samples == 'dog')}")
print(f"Number of cats that model predicts are in sample: {np.sum(predictions == 'cat')}")

total = len(samples)
TP = np.sum((samples == "cat") & (predictions == "cat")) # True Positives
TN = np.sum((samples == "dog") & (predictions == "dog")) # True Negatives
FP = np.sum((samples == "dog") & (predictions == "cat")) # False Positives
FN = np.sum((samples == "cat") & (predictions == "dog")) # False Negatives
accuracy = (TP + TN) / total
print(f"Accuracy = ({TP} + {TN}) / {total} = {accuracy}")

Number of cats in sample: 60
Number of dogs in sample: 40
Number of cats that model predicts are in sample: 85
Accuracy = (60 + 15) / 100 = 0.75

For every photo of a cat, the model correctly categorizes the photo as cat. But notice that the model also incorreclty categorizes 15 dog photos as cat. Do you think that the accuracy score sufficiently captures the model’s performance?

Precision

Formula

\[\dfrac{\text{True Positives}}{\text{Total number of "yes" predictions}}\]

Interpretation

Reveals when the model has a bias towards saying “yes”. Precision includes a penalty for misclassifying negative samples as positive. This is useful when the cost of misclassifying a negative sample as positive is high. For example, in fraud detection.

Example

precision = TP / (TP + FP)
print(f"Accuracy = ({TP} + {TN}) / {total} = {accuracy}")
print(f"Precision = {TP} / ({TP} + {FP})", f"{precision:.2f}")

Accuracy = (60 + 15) / 100 = 0.75
Precision = 60 / (60 + 25) 0.71

The precision score is 0.7. This means that the model is correct 70% of the time when it predicts “cat”. This is lower than the accuracy of .75 because the model is being penalized for misclassifying dog photos as cat photos. Do you think that this improves upon the accuracy score?

Recall (aka Sensitivity)

Formula

\[\dfrac{\text{True Positives}}{\text{Total number of actual positive samples}}\]

interpretation

Reveals when the model has a bias for saying “no”. It includes a penalty for false negatives. This is useful when the cost of classifying a positive sample as negative is high, for example, in cancer detection.

Example

recall = TP / (TP + FN)
print(f"Recall = {TP} / ({TP} + {FN}) = {recall:.2f}")

Recall = 60 / (60 + 0) = 1.00

The recall score is 1.0 (100%!), which indicates that the model does NOT have a bias towards saying “no”. We can see this in the data, as the model doesn’t misclassify any cat photo as dog photos.

F1

The F1 score basically accuracy, precision, and recall into a single metric.

Formula

\[\dfrac{ \text{True Positives} }{ \text{True Positives} + \dfrac{1}{2} (\text{False Positives} + \text{False Negatives}) }\]

The denominator is True Positives plus the average of the “two ways of being wrong”.

Interpretation

The F1 provides a balance between precision and recall. It gives a general idea of whether the model is biased (but doesn’t tell you which way it is biased). An F1 score is high when the model makes few mistakes.

Example

f1 = TP / (TP + (np.mean(FP + FN)))
print(f"F1 = {TP} / ({TP} + (1/2)*({FP} + {FN})) = {f1:.2f}")

F1 = 60 / (60 + (1/2)*(25 + 0)) = 0.71

Summary

As a reminder, here are the scores we calculated:

print(f"Accuracy = {accuracy:.2f}")
print(f"Precision = {precision:.2f}")
print(f"Recall = {recall:.2f}")
print(f"F1 = {f1:.2f}")

Accuracy = 0.75
Precision = 0.71
Recall = 1.00
F1 = 0.71

The F1 score is 0.71, do o you think this provides a good balance between precision, recall, and accuracy?

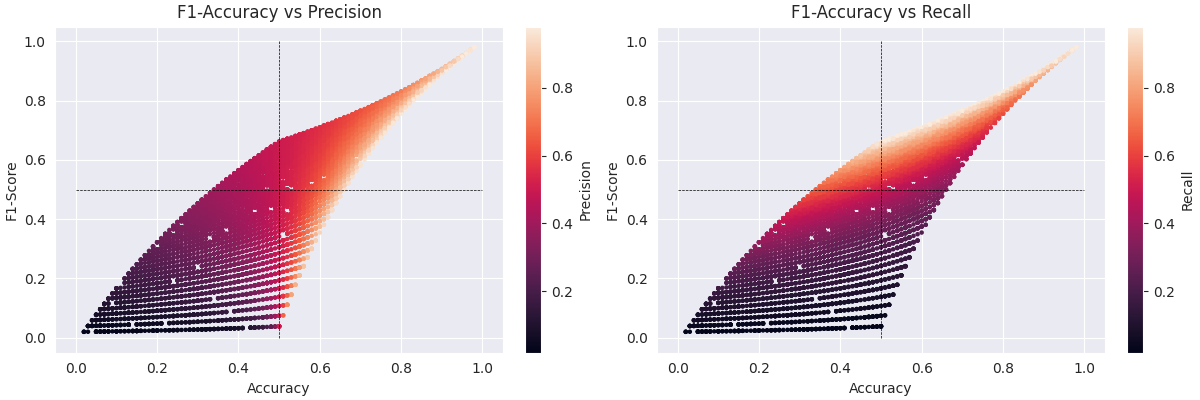
Visualizing the relationship between, accuracy, precision, recall, and F1

People often say that the F1 score is a “harmonic mean” of precision and recall. One way to think of this, is that the F1 score will penalize the model for being biased towards saying “yes” or “no”.

See also

Stack Overflow: Harmonic Mean

import libraries

import matplotlib.pyplot as plt
import seaborn as sns

# Let's run an experiment
n = 50
n_experiments = 10_000
# initialize arrays to store the results
accuracies = np.zeros(n_experiments)
precisions = np.zeros(n_experiments)
recalls = np.zeros(n_experiments)
f1_scores = np.zeros(n_experiments)

# run the experiment
for experiment in range(n_experiments):
    # generate random data
    tp = np.random.randint(1, n)
    fn = n - tp
    fp = np.random.randint(1, n)
    tn = n - fp

    # calculate metrics
    accuracies[experiment] = (tp + tn) / (2*n)
    precisions[experiment] = tp / (tp + fp)
    recalls[experiment] = tp / (tp + fn)
    f1_scores[experiment] = tp / (tp + (fp + fn) / 2)

# plot the results
sns.set_style("darkgrid")
fig, axes = plt.subplots(1, 2, figsize=(12, 4), constrained_layout=True)

for this_ax, metric, title in zip(axes, [precisions, recalls], ["Precision", "Recall"]):
    sc = this_ax.scatter(accuracies, f1_scores, c=metric, s=5)
    this_ax.plot([0, 1], [.5, .5], color="black", linestyle="--", linewidth=.5)
    this_ax.plot([.5, .5], [0, 1], color="black", linestyle="--", linewidth=.5)
    this_ax.set_title(f"F1-Accuracy vs {title}")
    this_ax.set_xlabel("Accuracy")
    this_ax.set_ylabel("F1-Score")
    # Add colorbar
    cbar = fig.colorbar(sc, ax=this_ax)
    cbar.set_label(title)
plt.show()

When Precision, Recall, and F1 are the same

When would precision and recall be the same? Let’s remind ourselves of the formulas:

Precision	Recall	F1 Score
\(\dfrac{TP}{TP + FP}\)	\(\dfrac{TP}{TP + FN}\)	\(\dfrac{TP}{TP + \text{mean(FP + FN)}}\)

When will these fractions be equal? Well they only differ in the denominator, in that precision cares about False Positives, recall cares about False Negatives, and F1 weighs them equally (it takes an average). So, if their denominators are equal, then the fractions will be equal. Put differently, if the model makes the same number of False Positives as False Negatives, then it doesn’t have a bias towards saying “yes” or “no”.

To add one more layer of complexity, if precision and recall are equal, then surely the F1 score will be equal to them as well.. Because the average of two equal numbers is the same as the numbers themselves. This makes the F1 fraction equal to both the precision and recall fractions.

To drive that point home, let’s provide an example in code:

from sympy import symbols, solve, simplify

# Define variables for confusion matrix
tp, tn, fp, fn = symbols('tp tn fp fn')

# Basic metrics
accuracy = (tp + tn) / (tp + tn + fp + fn)
precision = tp / (tp + fp)
recall = tp / (tp + fn)
f1 = 2 * (precision * recall) / (precision + recall)

# Try to solve system of equations
# We want the number of true positives to be equal to the number of false negatives
solution = solve([
    fp - fn
])

print("Solution space:")
print(solution)

print("\nMetrics in terms of remaining variables:")
print(f"Precision = {simplify(precision.subs(solution))}")
print(f"Recall = {simplify(recall.subs(solution))}")
print(f"F1 Score = {simplify(f1.subs(solution))}")

Solution space:
{fn: fp}

Metrics in terms of remaining variables:
Precision = tp/(fp + tp)
Recall = tp/(fp + tp)
F1 Score = tp/(fp + tp)